Bias-Variance Tradeoff

03 May 2018

"In statistics and machine learning, the bias-variace tradeoff is the problem of simultaneously minimizing two sources of error that prevent supervised learning algorithms from generalizing beyond their training set."

Bias and Variance Tradeoff

통계학과 머신러닝에서 예측모형에 대해서 이야기할 때, 예측 에러는 크게 두가지 부분으로 나뉜다: “Bias(편향)”에 의한 에러와 “Variance(분산)”에 의한 에러. 그러나 불행하게도 Bias-variance tradeoff로 인해 양 쪽 모두를 동시에 줄일 수 없으며 또한 이는 모형의 Overfitting(과적합) 또는 Underfitting(과소적합) 문제와도 연결된다. 따라서 뛰어난 모형은 편향과 분산의 총 합을 줄이기 위해 노력해야하며, 이 두 종류의 에러를 이해하는 것은 결국 Over/Under fitting의 실수를 피하고 예측모형의 올바른 진단을 이끌어내는데 도움이 될 것이다.

Conceptual & Mathematical Definition

Error due to Bias: 편향에 의한 에러는 우리의 prediction function( $\hat {f}$ )과 찾고자 하는 ture function( $f$ )과의 차이로 인해 발생한다. 아래 수식을 보면 편향은 그 차이의 기댓값이(expected, average)임을 알 수 있는데, 그 이유는 다수의 샘플링된 데이터셋( $D_i$ )마다 다수의 prediction function( $\hat {f_i}$ )이 존재하기 때문이다.
즉 편향은 알고리즘을 학습하는데 있어서 가정 및 학습의 방향성을 의미한다고 볼 수 있으며, 만약 편향에 의한 에러가 크다면 잘못된 방향으로의 학습을 뜻하고, 우리의 prediction function이 주어진 데이터셋에서 features와 target간의 관계를 잘 파악하지 못한 것이라 할 수 있다. (Underfitting)

$\operatorname {Bias} {\big [}{\hat {f}}(x){\big ]}=\operatorname {E} {\big [}{\hat {f}}(x)-f(x){\big ]}$

Error due to variance: 분산에 의한 에러는 주어진 우리의 prediction function들의 다양한 정도, 분산의 정도에 의해 발생한다. 다시말해 실제값(actual point)에 대하여 우리의 prediction function들이 얼마나 다양한 범위로 예측을 하는지이다.
즉 분산은 알고리즘을 학습하는데 있어서 학습의 일관성을 의미한다고 볼 수 있으며, 만약 분산에 의한 에러가 크다면 각각의 알고리즘 학습이 일관성 없이 중구난방으로 이뤄졌음을 뜻하고, 우리의 prediction funtion이 학습용 데이터(training data)에 포함된 노이즈까지 학습한 것이라 볼 수 있다. (Overfitting)

$\begin{align} \operatorname {Var} {\big [}{\hat {f}}(x){\big ]}= & \operatorname {E} {\big [} (\hat {f}(x) - \operatorname{E}[\hat{f}(x)])^2{\big ]} \\ & \operatorname {E} [{\hat {f}}(x)^{2}]-\operatorname {E} [{\hat {f}}(x)]^{2} \\ \end{align}$

Graphical Definition

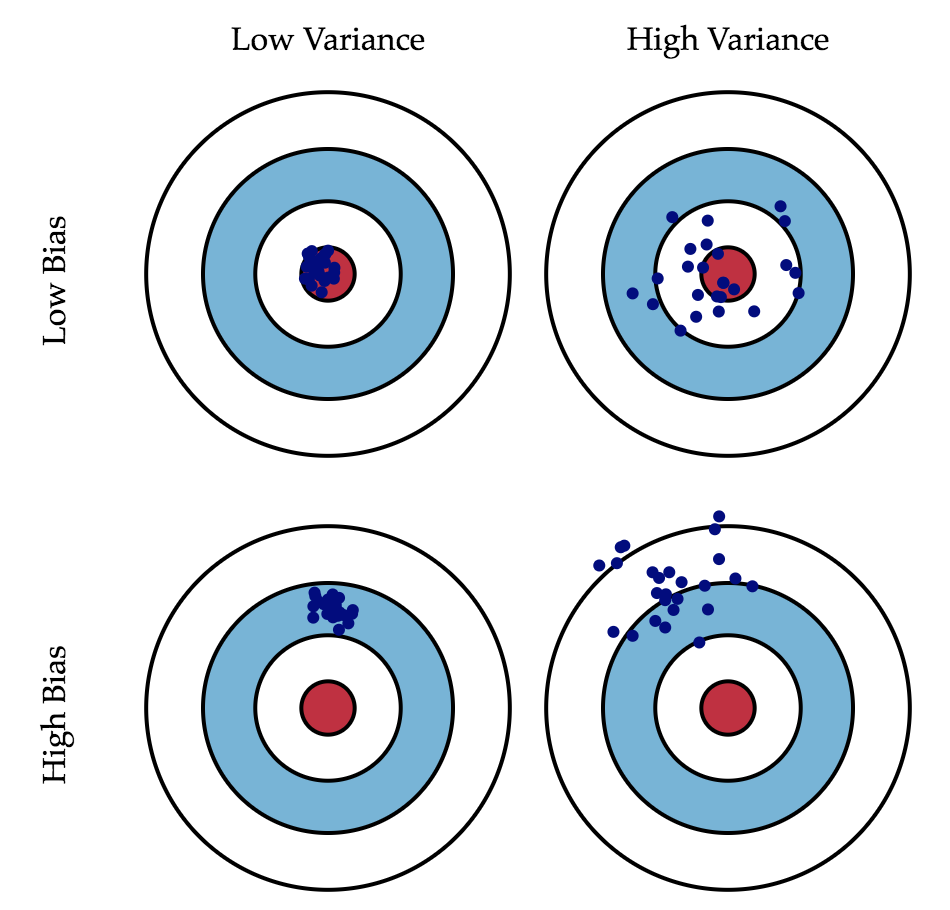
편향과 분산에 대해서 직관적으로 파악할 수 있는 bulls-eye diagram을 보자. 중앙의 빨간색 목표물이 바로 우리의 모델이 예측해야하는 실제값( $y$ )이며, 목표물에서 멀어지면 멀어질 수록 예측력이 점점 더 나빠짐을 의미한다. 파란색 점들은 샘플링된 여러 데이터셋에 대한 prediction model들의 예측값( $y_i$ , when $i$ is # of models)들을 의미한다.
편향의 정도에 따라 파란색 점들이 빨간색 목표물로 부터 얼마나 떨어져 있는지를 확인할 수 있고, 분산의 정도에 따라 파란색 점들이 얼마나 흩어져 있는지를 확인할 수 있다.

Bias-Variance Decomposition

우리의 훈련용 데이터는 $x_1, \cdots, x_n$ 개의 data point가 있고, 각각의 $x_i$ 에 해당하는 실제값 $y_i$ 가 존재한다. 그리고 우리는 다음과 같이 랜덤 노이즈가 섞인 함수 관계로 표현할 수 있다.

$y = f(x) + \varepsilon, \text{where the noise} ~ \varepsilon \sim \mathcal{N}(0, \sigma^2)$

우리의 목표는 이 true function $f$ 에 가능한 가장 근접한 prediction function $\hat{f}$ 를 찾는 것이며, 이는 $y$ 와 $\hat{f}$ 의 mean squared error를 최소화하는 문제를 품으로써 구할 수 있다. 물론 주어진 $x_1, \cdots, x_n$ 뿐만 아니라 주어진 샘플 밖의 data points 에 대해서도 말이다. 그러나 $y_i$ 가 갖고있는 랜덤 노이즈( $\varepsilon$ ; irreducible error) 때문에 완벽한 $\hat{f}$ 를 찾는건 불가능함을 알아야 한다.

$\min \sum{ \big[ (y - \hat{f})^2 \big] }$

일반화된 $\hat{f}$ 를 찾는 것은 다수의 샘플링된 데이터셋에 대한 다수의 알고리즘에 의해 진행되기 때문에, 우리가 어떤 $\hat{f}$ 를 선택하든지 간에 unseen sample(=test set) $x$ 에 대한 기대오차(expected error)를 구할 수 있고, 이는 아래와 같이 분해가 된다.

${\begin{aligned}\operatorname {E} {\Big [}{\big (}y-{\hat {f}}(x){\big )}^{2}{\Big ]}&=\operatorname {Bias} {\big [}{\hat {f}}(x){\big ]}^{2}+\operatorname {Var} {\big [}{\hat {f}}(x){\big ]}+\sigma ^{2}\\\end{aligned}}$ $(\text{mse}_{testset} = \text{Bias}^2 + \text{Variance} + \text{irreducible error})$

Derivation

먼저 유도과정에 사용되는 수식을 나열하면 다음과 같다.

i. 분산식의 재정렬

${\begin{aligned}\operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2} \Longleftrightarrow \operatorname {E} [X^{2}]=\operatorname {Var} [X]+\operatorname {E} [X]^{2}\end{aligned}}$

ii. $y$ 의 기댓값
ture function $f$ 는 deterministic(결정된 함수)이므로 $\operatorname{E}[f] = f$ 이다.
irreducible error $\varepsilon \sim \mathcal{N}(0, \sigma^2)$ 이므로 $\operatorname{E} [\varepsilon] = 0$ 이다. 따라서,

${\displaystyle \operatorname {E} [y]=\operatorname {E} [f+\varepsilon ]=\operatorname {E} [f]=f}.$

iii. $y$ 의 분산
$\operatorname{Var} [\varepsilon] = \sigma^2$ 이며, (i) & (ii) 에 의해,

${\begin{aligned}\operatorname {Var} [y]&=\operatorname {E} [(y-\operatorname {E} [y])^{2}]=\operatorname {E} [(y-f)^{2}]\\&=\operatorname {E} [(f+\varepsilon -f)^{2}]=\operatorname {E} [\varepsilon ^{2}]\\&=\operatorname {Var} [\varepsilon ]+\operatorname {E} [\varepsilon ]^{2}\\&=\sigma ^{2}\end{aligned}}$

따라서 Bias-Variance Decomposition은 다음과 같이 쓸 수 있다.

${\begin{aligned}\operatorname {E} {\big [}(y-{\hat {f}})^{2}{\big ]}&=\operatorname {E} [y^{2}+{\hat {f}}^{2}-2y{\hat {f}}]\\&=\operatorname {E} [y^{2}]+\operatorname {E} [{\hat {f}}^{2}]-\operatorname {E} [2y{\hat {f}}]\\&=\operatorname {Var} [y]+\operatorname {E} [y]^{2}+\operatorname {Var} [{\hat {f}}]+\operatorname {E} [{\hat {f}}]^{2}-2f\operatorname {E} [{\hat {f}}]\\&=\operatorname {Var} [y]+\operatorname {Var} [{\hat {f}}]+(f^{2}-2f\operatorname {E} [{\hat {f}}]+\operatorname {E} [{\hat {f}}]^{2})\\&=\operatorname {Var} [y]+\operatorname {Var} [{\hat {f}}]+(f-\operatorname {E} [{\hat {f}}])^{2}\\&=\sigma ^{2}+\operatorname {Var} [{\hat {f}}]+\operatorname {Bias} [{\hat {f}}]^{2}\\&=\text{irreducible error} + \text{Variance} + \text{Bias}^2\end{aligned}}$

Simulation of Bias-Variance Tradeoff

Polynomial Regression에서 모형의 복잡도를 결정하는 것은 degrees of polynomial 이다. Over/Under fitting 을 방지하고 모형의 제대로된 학습을 위해선 degrees of polynomial 을 잘 조정해야하며, 이 값이 변함에 따라 편향과 분산은 어떻게 변하는지 확인할 수 있다.
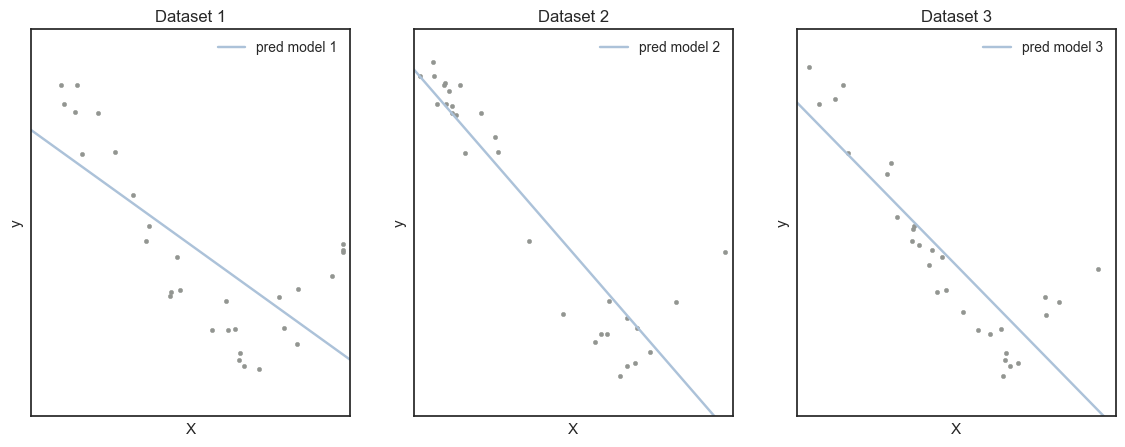
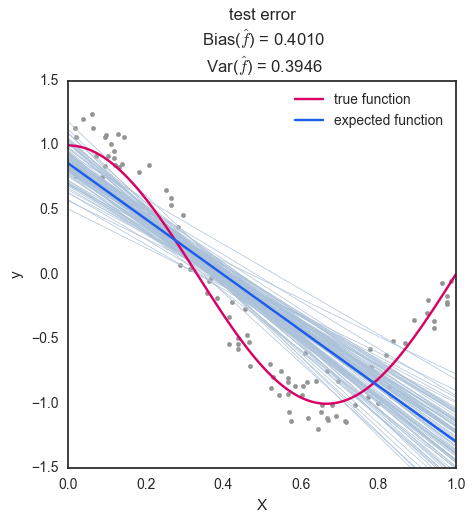
그림에서 회색 점은 실제값( $y_i$ )를 나타내며, 빨간색 선이 우리가 찾고자 하는 true function( $f$ )이다. 연한 파란색 선은 개별 prediction function( $f_1, \cdots, f_n$ )이며, 진한 파란색 선은 N개의 prediction functions의 평균인 expected prediction function( $\operatorname{E}[\hat(f)]$ )을 나타낸다.

degree = 1: degree 가 1인 경우 편향은 0.4010으로 다소 높은 값을 가지며, 분산은 0.3946으로 낮은 값을 갖는다. 이는 $\hat{f}$ 가 너무 단순하여 주어진 데이터에 대해 학습이 제대로 이뤄지지 않았음을 보여준다. (Underfitting)

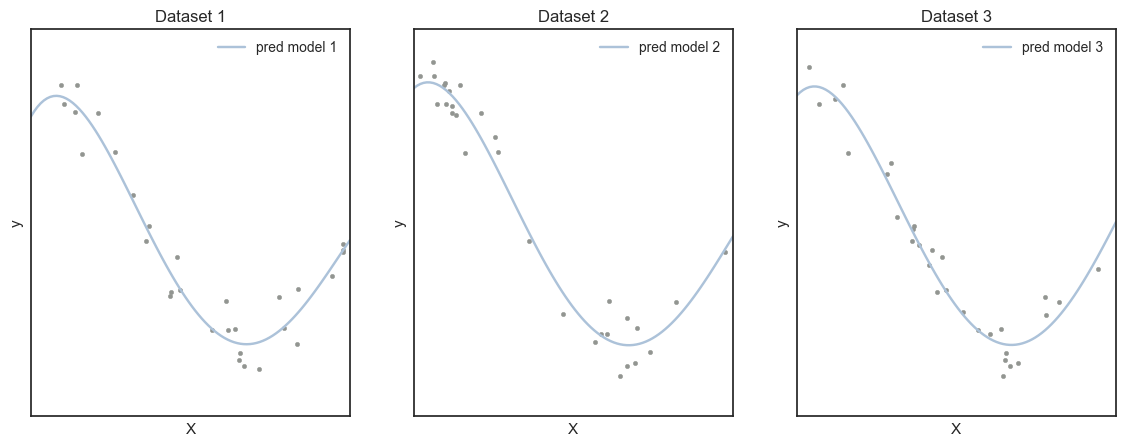
degree = 4: degree 가 4인 경우 편향은 0.1384로 degree 1 일 때보다 대폭 감소하였으며, 분산은 0.5529로 다소 증가하였다. 편향과 분산의 에러의 총 합을 보면 이전보다 0.1가량 줄어들어 $\hat{f}$ 가 주어진 데이터에 대해 학습이 잘 이뤄졌음을 볼 수 있다. (Well-fitted)

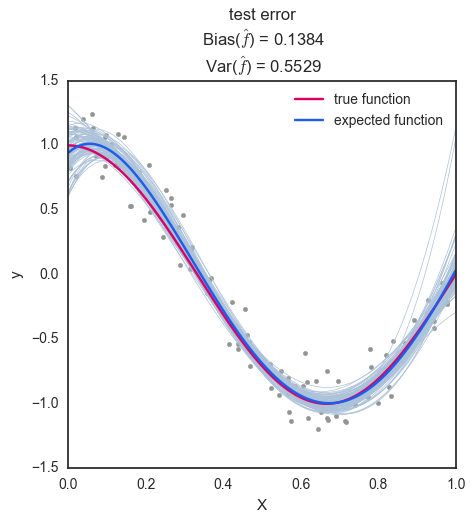
degree = 10: degree 가 10인 경우 편향은 0.3811으로 degree 4일때보다 높게 나왔지만 이는 샘플의 수가 충분치 않아 생기는 현상으로 일반적으로 편향은 감소하게 된다. 반면에 분산은 9.7537로 대폭 상승하였으며, 이는 $\hat{f}$ 가 너무 복잡하여 주어진 데이터가 가진 노이즈까지 학습하여 과적합이 이뤄졌음을 보여준다. (Overfitting)

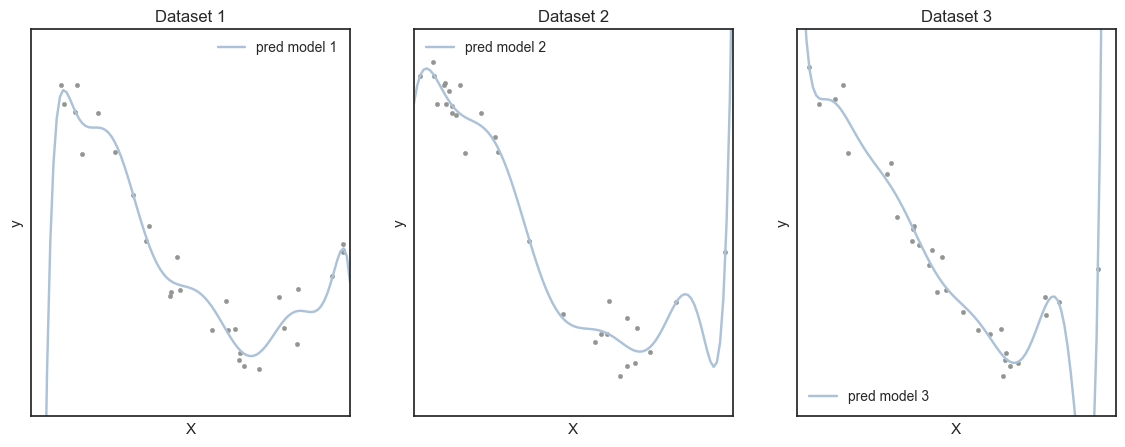
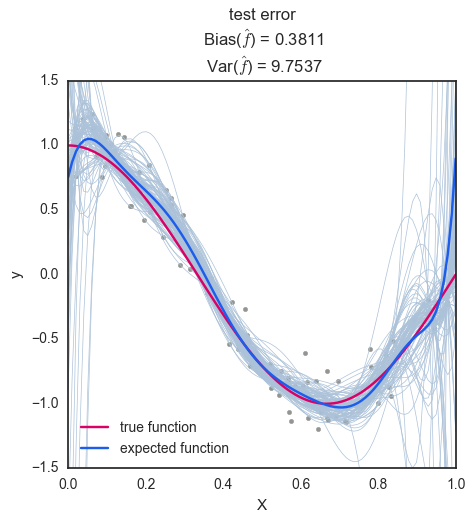
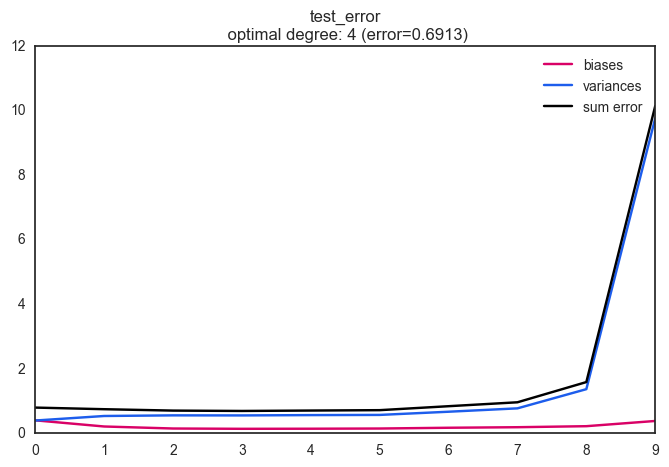
Train & Test Error: 일반적으로 모형의 복잡도가 증가할수록 Train Set에 대해서 에러는 감소한다. 그러나 우리에게 중요한 것은 주어진 데이터셋에 대해 예측력을 높이는 것이 아닌, 앞으로 모형을 활용할 Unseen Data에 대한 예측력이며 이는 Test Set에 대한 에러를 의미한다.
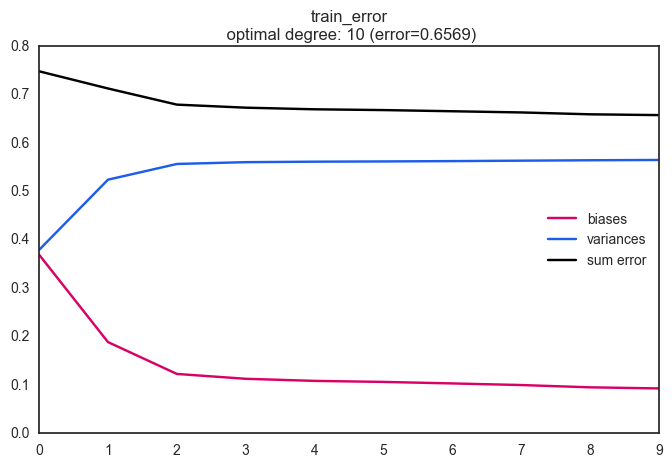
아래 그림에서와 같이 모형의 복잡도(Degree)가 증가할 수록 Train set에 대한 총 오차는 지속적으로 감소함을 볼 수 있고, Test set에 대한 총 오차는 degree = 4일때 최소가 되어 모형의 최적 degree는 4가 됨을 알 수 있다.

reference

code

github.com/JKeun